Índice
Introdução
Calcular o fator K correto, a tolerância de dobra e a dedução de dobra são cruciais para obter uma peça acabada de boa qualidade do seu hidráulico pressione o freio. O conhecimento e a técnica da prensa dobradeira são seus fundamentos, fundamentais para ajudá-lo a utilizá-la na fabricação.
Calcular o comprimento da planificação a partir da peça 3D não é tão difícil. Embora você possa encontrar várias fórmulas diferentes que pretendem calcular a tolerância de dobra, elas geralmente são a mesma fórmula, apenas simplificadas pelo preenchimento do ângulo ou de um fator K. Este artigo mostrará essas informações, incluindo o fator K, margem de dobra e dedução de dobra.
O que é tolerância de curvatura?
Os metais podem realmente ser dobrados. Na fabricação de chapas metálicas, o metal deve ser dobrado, não apenas para formar um determinado formato, mas também para cumprir as normas de segurança quando o metal é submetido a impactos, fazendo com que ele dobre em vez de quebrar. Independentemente do tipo de metal, bem como da forma e espessura do metal, cada peça de metal possui um certo grau de tolerância à flexão.
Definição de tolerância de dobra
A tolerância de dobra (BA) é o comprimento do arco de flexão medido ao longo do eixo neutro da placa de metal, uma vez que o comprimento do eixo neutro não muda após a flexão.
Uma vez calculada a tolerância de dobra, ela deve ser adicionada ao comprimento plano para determinar o comprimento da chapa metálica necessário para formar a peça de trabalho desejada.
Como calcular a tolerância de dobra
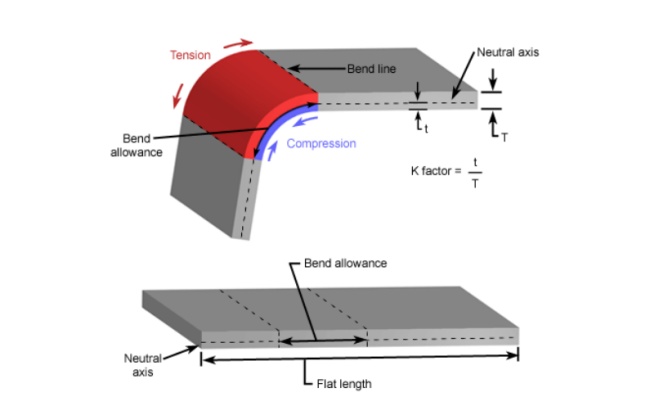
Como é mostrado na figura abaixo:
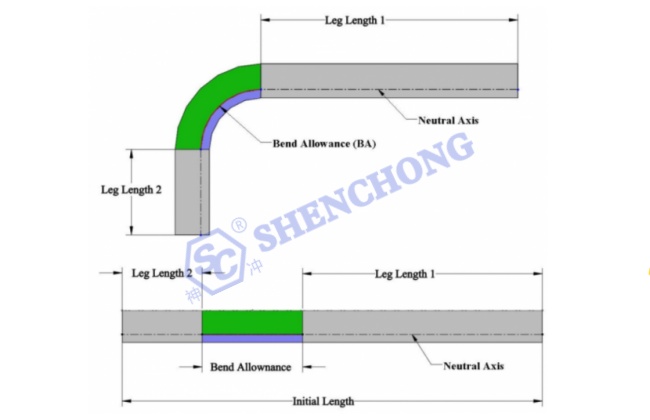
A seguinte fórmula é usada para calcular o comprimento plano:
Comprimento plano de chapa metálica = Comprimento da perna 1 +BA + comprimento da perna 2
Fórmula de cálculo de tolerância de dobra
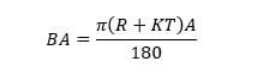
A – Ângulo de curvatura
R – Raio interno
K – Fator K
T – Espessura do material
Vamos começar com um colchete L simples. A imagem mostra que as pernas do suporte têm 2” e 3”. A espessura do material é 0,125”, o raio interno é 0,250” e o ângulo de curvatura é 90 graus. O comprimento plano é o total da porção plana de ambos os flanges mais o comprimento através do arco da área dobrada. Mas você calcula isso por dentro ou por fora do material? Nenhum! É aqui que o fator K entra em jogo. O fator K é a porcentagem da espessura do material onde não há estiramento ou compressão do material, por exemplo, o eixo neutro. Para este colchete L simples, usarei um fator K de 0,42.
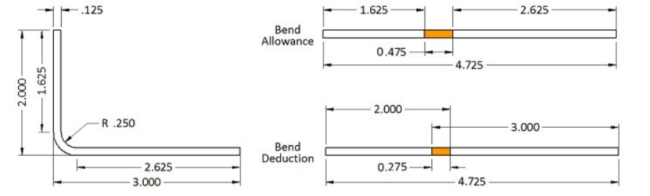
Usando a fórmula acima, temos: Tolerância de dobra = 90 * (π / 180) * (0,250 + 0,42 * 0,125) = 0,475″.
Portanto, o comprimento da planificação é 1,625” + 2,625” + 0,475″, que é igual a 4,725″. Portanto, se você somar o comprimento plano de todos os flanges e adicionar uma tolerância de dobra para cada área de dobra, terá o comprimento plano correto da peça.
Mas olhe o desenho. Não é assim que normalmente dimensionamos uma peça de chapa metálica. As dimensões são geralmente até a interseção dos flanges ou da Linha do Molde. Isso significa que temos que subtrair duas vezes a espessura do material mais o raio de dobra (também conhecido como recuo) para cada área de dobra. Para este conjunto de dimensões, seria mais fácil calcular o valor da Compensação de Dobra. O valor de Compensação de dobra permite somar o comprimento de cada flange usando as dimensões da Linha do molde e, em seguida, adicionar uma Compensação de dobra por área de dobra ao total. É -0,275, um número negativo, o que significa que você subtrairá esse valor do total dos comprimentos do flange, 5”, para obter 4,725″.
O que é fator K?
O fator k é a porcentagem da espessura do material onde não há estiramento ou compressão do material na área de dobra.
Quanto mais duro for o material, menor será a compressão no interior da dobra. Portanto, há mais alongamento do lado de fora e o eixo neutro se move em direção ao interior da curva. Materiais mais macios permitem maior compressão no interior e o eixo neutro permanece mais próximo do centro da espessura do material.
O raio de curvatura tem um efeito semelhante. Quanto menor o raio da curvatura, maior será a necessidade de compressão e o eixo neutro se moverá em direção ao interior da curvatura. Em um raio maior. o eixo neutro permanece próximo ao centro da espessura do material.
Para entender o fator K, precisamos primeiro entender o eixo neutro.
Quando a chapa metálica é dobrada, a superfície inferior é comprimida e a superfície superior é esticada. O eixo neutro está localizado dentro do metal onde não será comprimido nem expandido, permitindo manter um comprimento constante.
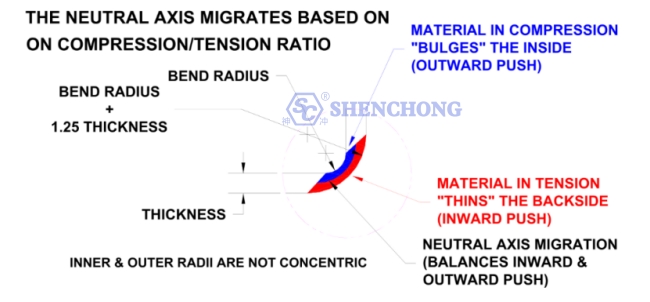
Eixo neutro
O eixo neutro não muda. Ao desenvolver um comprimento de peça plana, há um comprimento da peça que não muda. Esse comprimento é chamado de eixo neutro. O material na parte interna do eixo neutro será comprimido, enquanto o material na parte externa será esticado. Com base na espessura do material, no raio da forma e nos métodos de conformação, a relação entre compressão e tensão na peça mudará.
Uma peça que é dobrada sobre um raio muito acentuado, quando comparada à espessura, esticará mais do lado de fora, o que significa que o eixo neutro ficará mais próximo do interior da dobra. Uma peça que é gradualmente dobrada terá menos alongamento externo, o que significa que o eixo neutro ficará mais próximo do centro da peça.
Em chapas planas, o eixo neutro está localizado uniformemente na metade da espessura da chapa, mas se moverá durante a flexão.
A mudança de posição do eixo neutro é determinada por vários fatores, como propriedades do material, espessura, ângulo de curvatura, raio interno e método de curvatura da placa.
Como calcular fatores K
Matematicamente, o fator K representa a razão entre a posição do eixo neutro (t) e a espessura da placa (T).
Fórmula de Fatores K
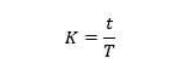
Onde t é a distância da superfície interna ao eixo neutro e T é a espessura do metal.
O fator K é determinado pelas propriedades físicas do material, método de dobra, ângulo de dobra e outros fatores.
O valor dos fatores K estará sempre entre 0 e 1. Se um fator k for 0,25, significa que o eixo neutro está localizado em 25% da espessura do material da chapa metálica da peça. Da mesma forma, se for 0,5, significa que o eixo neutro está localizado em 50% de toda a espessura.
Propriedades dos materiais: normalmente varia entre 0,30 e 0,50. Em geral, o fator K de cobre macio ou materiais de cobre macio é 0,35, o fator K de materiais como cobre semiduro ou latão, aço macio e alumínio é 0,41, e o fator K de materiais como bronze, cobre duro, aço laminado a frio e aço para molas é 0,45.
Raio de curvatura: quanto menor o raio de curvatura, maior o fator K.
Espessura do material: quanto maior a espessura do material, maior o fator K.
Força de escoamento do material: quanto maior o limite de escoamento, menor o fator K.
Módulo elástico (também conhecido como módulo de Young): quanto maior a espessura do material, maior o fator K.
Na fabricação de chapas metálicas de precisão usando Prensa dobradeira CNC, o fator K é um fator crucial. O fator K é usado para calcular o padrão plano de dobra, que está diretamente relacionado ao comprimento da chapa esticada durante a dobra.
É o valor fundamental para determinar a tolerância à flexão e a dedução da flexão.
Como a relação entre a distância ao eixo neutro e a espessura da placa determina a posição do eixo neutro na placa metálica, conhecer o fator K ajuda a determinar a posição do eixo neutro após a flexão.
Fatores K para alumínio e aço
Você também pode determinar o fator K usando a tabela abaixo:
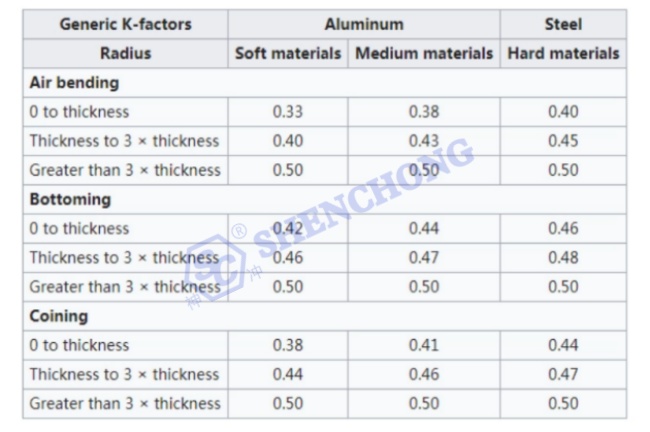
Fatores K para cobre, latão e bronze
Após um estudo cuidadoso, descobriu-se que o sistema SolidWorks também fornece algoritmos de compensação de flexão para os seguintes materiais específicos em um ângulo de flexão de 90 graus. A fórmula de cálculo específica é a seguinte:
Material de latão macio ou cobre macio: BA=(0,55 * T)+(1,57 * R)
Materiais como cobre semi-duro ou latão, aço macio e alumínio: BA=(0,64 * T)+(1,57 * R) Materiais como bronze, cobre duro, aço laminado a frio e aço para mola: BA=(0,71 * T)+(1,57 * R) Na verdade, se simplificarmos a equação (7) e definirmos o ângulo de flexão para 90 graus e calcularmos a constante, a equação pode ser transformada em:
BA = (1,57 * K * T) + (1,57 * R)
Assim, para materiais de latão macio ou cobre macio, comparando a fórmula de cálculo acima, podemos obter 1,57xK=0,55K=0,55/1,57=0,35. É fácil calcular os valores do fator k de vários tipos de materiais listados no livro usando o mesmo método.
Material de latão macio ou cobre macio: K = 0,35.
Materiais como cobre semi-duro ou latão, aço macio e alumínio: K=0,41.
Materiais como bronze, cobre duro, aço laminado a frio e aço para molas: K = 0,45.
O que é dedução de curvatura?
Ao dobrar chapas metálicas, devido à deformação plástica incompleta do material e às limitações estruturais da própria máquina-ferramenta, o ângulo e o comprimento da peça dobrada podem divergir das dimensões projetadas. Para garantir que a precisão da dobra e o tamanho da peça atenda aos requisitos, é necessário considerar a dedução da dobra durante a produção do desenho, ou seja, reduzir o tamanho da dobra que precisa ser feita.
Definição de dedução de dobra
A dedução da dobra é o comprimento do material que precisamos remover do comprimento total da placa para obter o padrão plano correto.
Princípio de dedução de curvatura
O princípio da dedução da flexão é utilizar a deformação elástica do material, de modo que o comprimento e o ângulo após a flexão possam atender aos requisitos do projeto. Ao dobrar, a chapa metálica é colocada na máquina dobradeira, que aplica força de dobra para causar deformação elástica da chapa metálica, resultando em mudanças na forma e no ângulo e, por fim, tornando-se a forma desejada. Neste processo, a dedução da flexão pode ser controlada com precisão ajustando o tamanho do desenho, atingindo a precisão e o tamanho exigidos pelo projeto.
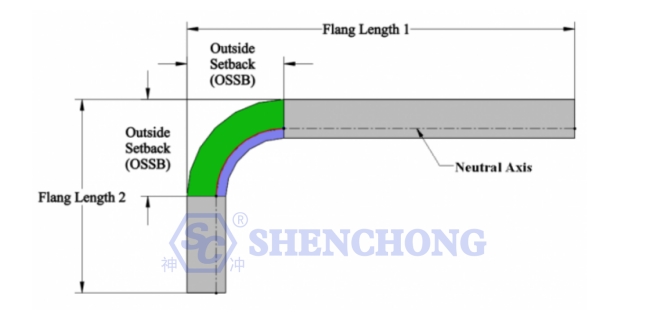
De acordo com a figura acima, a dedução da dobra é a diferença entre a tolerância de dobra e o dobro do recuo externo.
Fórmula de cálculo de dedução de dobra
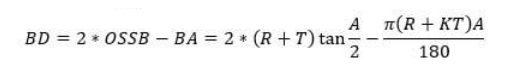
Onde:
OSSB – O recuo externo (o comprimento da peça que se estende além do ângulo de dobra).
R – Raio de curvatura
K – Fator K (determinado pelas propriedades e espessura do material)
T – Espessura do material
A – Ângulo de curvatura desejado em graus
Vamos supor que queremos dobrar uma chapa de aço inoxidável com 2 mm de espessura em um ângulo de 90° com um raio de curvatura interno de 3 mm. O fator K para este material é conhecido como 0,44. Vamos calcular a dedução de curvatura passo a passo:
- Calcule a tolerância de dobra (BA):
BA = π * (R + K * T) * (A/180)
Onde R é o raio de dobra interno, K é o fator K, T é a espessura da chapa e A é o ângulo de dobra.
Conectando os valores:
BA = π * (3 + 0,44 * 2) * (90/180) = 4,39 mm
- Calcule o Recuo Externo (OSSB):
OSSB = R + T = 3 + 2 = 5mm
- Calcule a dedução de curvatura (BD):
BD = 2 * OSSB – BA
Conectando os valores:
BD = 2 * 5 – 4,39 = 5,61 mm
Portanto, para obter uma dobra de 90° com um raio de curvatura interno de 3 mm nesta chapa de aço inoxidável de 2 mm de espessura, precisamos definir a Dedução de Dobra para 5,61 mm durante o processo de dobra.
Isso significa que precisamos dobrar demais a folha em 5,61 mm para compensar o retorno elástico após a dobra, alcançando finalmente o ângulo de dobra desejado de 90°.
O cálculo da dedução da dobra pode ajudar a determinar as dimensões da peça antes da dobra, permitindo um melhor planejamento da produção e redução do desperdício de material.
Principais funções da dedução de flexão
- Garanta a precisão da dobra. A dedução de dobra pode controlar o comprimento e o ângulo da chapa dobrada, garantindo assim que as peças de chapa produzidas atendam aos requisitos de tamanho e precisão do projeto.
- Melhore a eficiência do processamento. O projeto de dedução de flexão não apenas reduz o tamanho da produção, mas também evita experimentos e ajustes repetidos, melhorando assim a eficiência da fabricação de peças de chapa metálica.
- Reduza o desperdício de materiais. Ao usar a dedução de flexão para controlar as dimensões, o processamento excessivo ou o desperdício de material podem ser evitados, reduzindo assim os custos e melhorando a eficiência da produção.
Resumindo, a dedução da flexão é um elo muito importante no processo de processamento de chapas metálicas e também a chave para garantir a qualidade e precisão do produto acabado. No processamento real, o valor da dedução de flexão deve ser ajustado razoavelmente de acordo com a situação específica para obter o melhor efeito de processamento.
Materiais com diferentes tolerâncias de curvatura
Que metal pode dobrar bem?
Todos os metais possuem um certo grau de elasticidade. Alguns metais são mais elásticos que outros e podem atingir maiores tolerâncias de flexão em comparação com outros materiais. Os metais são classificados de acordo com seu módulo de elasticidade, que é a razão entre tensão e deformação na deformação do metal. O módulo elástico também é um meio de medir a rigidez do material ou a resistência elástica. Outros materiais como borracha e vidro também podem ser calculados da mesma forma.
Surpreendentemente, um dos metais mais elásticos é o níquel titânio, também conhecido como níquel titânio, com pressão de 28 GPa. Pode ser apertado muitas vezes sem ser considerado deformado. Entre os tipos de metais comuns, os segundos maiores metais elásticos incluem 45 GPa de estanho, magnésio, cádmio e 69 GPa de alumínio. É claro que o alumínio é conhecido por sua leveza e capacidade de flexão, mas em termos de metais puros, incluindo ligas, existem alguns metais que podem superá-lo nesse aspecto.
Quais metais não podem dobrar bem ou fraturarão quando dobrados demais?
Como é bem sabido, a maioria dos metais é muito dura e, se o material não for dobrado, certamente quebrará quando dobrado. Dentre todas as ligas, o tungstênio é o metal mais duro, podendo atingir até 411 GPa. Mesmo na sua forma mais fina, o tungstênio é difícil de dobrar, por isso é provável que quebre como o vidro. O segundo metal mais duro é o cobre-berílio 304GPa. O cromo é um material encontrado em diamantes e outras pedras preciosas, ocupando o terceiro lugar com 279 GPa. Ferro forjado e cobalto têm 211 GPa. A 210GPa, você tem muito mais chapas metálicas comuns, como aço, aço inoxidável, cobalto e níquel. Como você sabe, a maioria dos metais são considerados muito duros, mas como mencionado anteriormente, alguns metais não são tão duros quanto outros.
Conclusão
O fator K, também conhecido como fator do raio de curvatura, é responsável pela tendência do material de esticar na superfície externa e comprimir na superfície interna durante a flexão.
O cálculo adequado do fator K é importante para determinar a posição do eixo neutro e minimizar possíveis defeitos como rachaduras ou enrugamentos.
A tolerância de dobra refere-se ao material adicional necessário para acomodar o raio de curvatura, evitando estiramento ou compressão excessivos do material.
O cálculo preciso da tolerância de dobra é vital para garantir que as dimensões finais da peça estejam alinhadas com as especificações do projeto.
A dedução de flexão, por outro lado, compensa o efeito elástico do material, onde a parte dobrada tende a se desdobrar parcialmente após a remoção da força de flexão.
A contabilização da dedução de dobra é essencial para atingir o ângulo de dobra desejado e manter a precisão dimensional.
Ao compreender e aplicar adequadamente esses fatores essenciais, você pode otimizar seus processos de dobra, minimizar o desperdício de material e produzir consistentemente componentes dobrados de alta qualidade que atendam aos requisitos mais rigorosos.





