Tabla de contenido
Introducción
Calcular el factor K correcto, el margen de curvatura y la deducción de curvatura son cruciales para obtener una pieza terminada de buena calidad de su hidráulico presiona el freno. El conocimiento y la técnica de la plegadora son sus fundamentos, que son fundamentales para ayudarle a utilizarla en la fabricación.
Calcular la longitud del plano a partir de la pieza 3D realmente no es tan difícil. Aunque puede encontrar varias fórmulas diferentes que pretenden calcular el margen de flexión, generalmente son la misma fórmula, solo que simplificada al completar el ángulo o un factor K. Este artículo le mostrará esta información, incluido el factor K, el margen de curvatura y la deducción de curvatura.
¿Qué es el margen de curvatura?
De hecho, los metales se pueden doblar. Al fabricar chapa, el metal debe doblarse, no sólo para darle una forma determinada, sino también para cumplir con las normas de seguridad cuando el metal se somete a impactos, haciendo que se doble en lugar de romperse. Independientemente del tipo de metal, así como de la forma y el grosor del metal, cada pieza de metal tiene un cierto grado de tolerancia a la flexión.
Definición de margen de curvatura
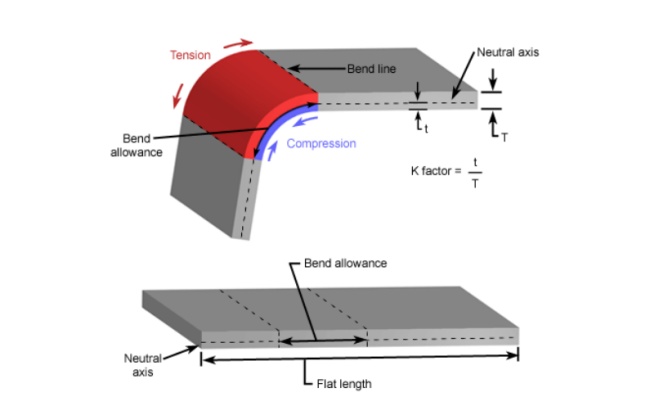
El margen de flexión (BA) es la longitud del arco de flexión medida a lo largo del eje neutro de la placa de metal, ya que la longitud del eje neutro no cambia después de la flexión.
Una vez que se calcula el margen de curvatura, se debe agregar a la longitud plana para determinar la longitud de chapa requerida para formar la pieza de trabajo deseada.
Cómo calcular el margen de curvatura
Como se muestra en la siguiente figura:
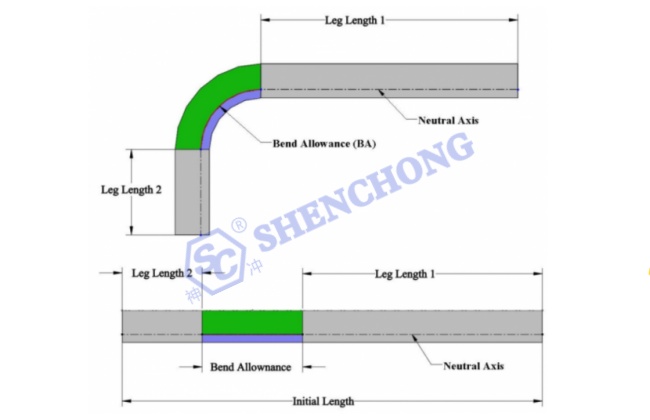
Se utiliza la siguiente fórmula para calcular la longitud plana:
Longitud de la chapa metálica = Largo de pierna 1 +BA + Largo de pierna 2
Fórmula de cálculo del margen de curvatura
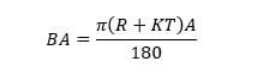
A – Ángulo de curvatura
R – Radio interior
K-factor K
T – Espesor del material
Comencemos con un soporte en L simple. La imagen muestra que las patas del soporte son de 2” y 3”. El espesor del material es 0,125”, el radio interior es 0,250” y el ángulo de curvatura es 90 grados. La longitud plana es el total de la porción plana de ambas bridas más la longitud a través del arco del área de curvatura. Pero, ¿calculas eso por el interior del material o por el exterior? ¡Ni! Aquí es donde entra en juego el factor K. El factor K es el porcentaje del espesor del material donde no hay estiramiento ni compresión del material, por ejemplo, el eje neutro. Para este soporte en L simple, usaré un factor K de 0,42.
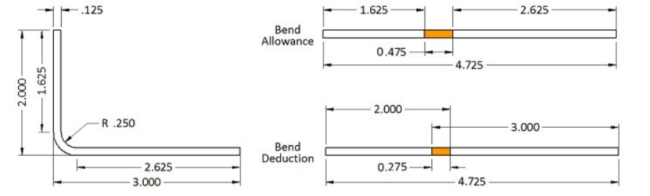
Al utilizar la fórmula anterior, tenemos: Margen de flexión = 90 * (π / 180) * (0,250 + 0,42 * 0,125) = 0,475”.
Entonces, la longitud del patrón plano es 1,625” + 2,625” + 0,475”, que es igual a 4,725”. Entonces, si suma la longitud plana de todas las bridas y agrega un margen de curvatura para cada área de curvatura, tendrá la longitud plana correcta de la pieza.
Pero mira el dibujo. Normalmente no dimensionamos así una pieza de chapa. Las dimensiones suelen ser hasta la intersección de las bridas o la línea del molde. Esto significa que tenemos que restar dos veces el espesor del material más el radio de curvatura (también conocido como retroceso) para cada área de curvatura. Para este conjunto de dimensiones, sería más fácil calcular el valor de Compensación de pliegue. El valor de Compensación de pliegue le permite sumar la longitud de cada pestaña usando las dimensiones de la Línea de molde y luego agregar una Compensación de pliegue por área de pliegue al total. Es -0,275, un número negativo, lo que significa que restarás esta cantidad del total de las longitudes de las bridas, 5 pulgadas, para obtener 4,725 pulgadas.
¿Qué es el factor K?
El factor k es el porcentaje del espesor del material donde no hay estiramiento ni compresión del material en el área de flexión.
Cuanto más duro es el material, menos compresión hay en el interior de la curva. Por lo tanto, se estira más en el exterior y el eje neutro se mueve hacia el interior de la curva. Los materiales más blandos permiten una mayor compresión en el interior y el eje neutro permanece más cerca del centro del espesor del material.
El radio de curvatura tiene un efecto similar. Cuanto menor sea el radio de curvatura, mayor será la necesidad de compresión y el eje neutro se moverá hacia el interior de la curvatura. En un radio mayor. el eje neutro permanece cerca del centro del espesor del material.
Para comprender el factor K, primero debemos comprender el eje neutro.
Cuando se dobla una lámina de metal, la superficie inferior se comprime y la superficie superior se estira. El eje neutro está ubicado dentro del metal donde no se comprimirá ni expandirá, lo que le permitirá mantener una longitud constante.
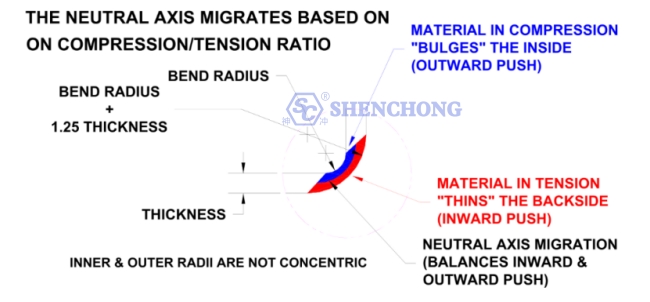
Eje neutral
El eje neutro no cambia. Al desarrollar una longitud en blanco plana, hay una longitud de la pieza que no cambia. Esta longitud se denomina eje neutro. El material en el interior del eje neutro se comprimirá, mientras que el material en el exterior se estirará. Según el radio de forma del espesor del material y los métodos de formación, la relación entre compresión y tensión en la pieza cambiará.
Una pieza que está doblada sobre un radio muy agudo, en comparación con el grosor, se estirará más en el exterior, lo que significa que el eje neutro estará más cerca del interior de la curvatura. Una pieza que se dobla gradualmente tendrá menos estiramiento exterior, lo que significa que el eje neutro estará más cerca del centro de la pieza.
En la chapa plana, el eje neutro está situado uniformemente a la mitad del espesor de la chapa, pero se moverá durante la flexión.
El cambio de posición del eje neutro está determinado por varios factores, como las propiedades del material, el espesor, el ángulo de flexión, el radio interno y el método de flexión de la placa.
Cómo calcular los factores K
Matemáticamente, el factor K representa la relación entre la posición del eje neutro (t) y el espesor de la placa (T).
Fórmula de factores K
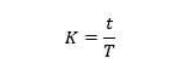
Donde t es la distancia desde la superficie interior al eje neutro y T es el espesor del metal.
El factor K está determinado por las propiedades físicas del material, el método de flexión, el ángulo de flexión y otros factores.
El valor de los factores K siempre estará entre 0 y 1. Si el factor k es 0,25, significa que el eje neutro se sitúa a 25% del espesor del material chapa de la pieza. Del mismo modo, si es 0,5 significa que el eje neutro se sitúa en 50% de todo el espesor.
Propiedades materiales: normalmente oscila entre 0,30 y 0,50. En general, el factor K de cobre blando o materiales de cobre blando es 0,35, el factor K de materiales como cobre o latón semiduro, acero dulce y aluminio es 0,41, y el factor K de materiales como bronce, cobre duro, acero laminado en frío y acero para resortes es 0,45.
Radio de curvatura: cuanto menor sea el radio de curvatura, mayor será el factor K.
Espesor del material: cuanto mayor es el espesor del material, mayor es el factor K.
Límite elástico del material: cuanto mayor es el límite elástico, menor es el factor K.
Módulo elástico (también conocido como módulo de Young): cuanto mayor es el espesor del material, mayor es el factor K.
En la fabricación de chapa de precisión mediante el uso Prensa plegadora CNC, el factor K es un factor crucial. El factor K se utiliza para calcular el patrón plano de flexión, que está directamente relacionado con la longitud de la chapa estirada durante la flexión.
Es el valor fundamental para determinar el margen de flexión y la deducción por flexión.
Dado que la relación entre la distancia al eje neutro y el espesor de la placa determina la posición del eje neutro en la placa de metal, conocer el factor K ayuda a determinar la posición del eje neutro después de la flexión.
Factores K para aluminio y acero
También puede determinar el factor K utilizando la siguiente tabla:
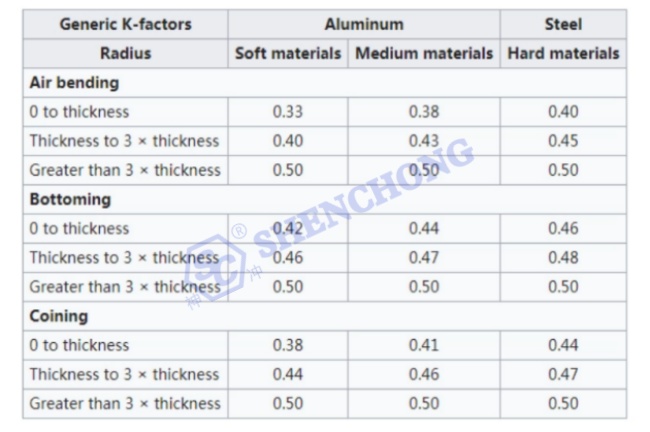
Factores K para cobre, latón y bronce
Después de un estudio cuidadoso, se descubrió que el sistema SolidWorks también proporciona algoritmos de compensación de flexión para los siguientes materiales específicos en un ángulo de flexión de 90 grados. La fórmula de cálculo específica es la siguiente:
Material de latón blando o cobre blando: BA=(0,55 * T)+(1,57 * R)
Materiales como cobre o latón semiduro, acero blando y aluminio: BA=(0,64 * T)+(1,57 * R) Materiales como bronce, cobre duro, acero laminado en frío y acero para resortes: BA=(0,71 * T)+(1.57 * R) En realidad, si simplificamos la ecuación (7) y establecemos el ángulo de flexión en 90 grados y calculamos la constante, la ecuación se puede transformar en:
BA=(1,57 * K * T)+(1,57 * R)
Entonces, para materiales de latón blando o cobre blando, al comparar la fórmula de cálculo anterior, podemos obtener 1,57xK=0,55K=0,55/1,57=0,35. Es fácil calcular los valores del factor k de varios tipos de materiales enumerados en el libro utilizando el mismo método.
Material de latón blando o cobre blando: K=0,35.
Materiales como cobre o latón semiduro, acero dulce y aluminio: K=0,41.
Materiales como bronce, cobre duro, acero laminado en frío y acero para resortes: K=0,45.
¿Qué es la deducción por curva?
Al doblar chapa, debido a la deformación plástica incompleta del material y a las limitaciones estructurales de la propia máquina herramienta, el ángulo y la longitud de la pieza doblada pueden diferir de las dimensiones previstas. Para garantizar que la precisión del doblado y el tamaño de la pieza de trabajo cumplan con los requisitos, es necesario considerar la deducción del doblado durante la producción del dibujo, es decir, reducir el tamaño del doblado que se debe realizar.
Definición de deducción de curvatura
La deducción de curvatura es la longitud de material que debemos eliminar de la longitud total de la placa para obtener el patrón plano correcto.
Principio de deducción de curvatura
El principio de la deducción por flexión es utilizar la deformación elástica del material, de modo que la longitud y el ángulo después de la flexión puedan cumplir con los requisitos de diseño. Al doblar, la chapa se coloca en la máquina dobladora, que aplica fuerza de flexión para provocar una deformación elástica de la chapa, lo que produce cambios en la forma y el ángulo y, en última instancia, adquiere la forma deseada. En este proceso, la deducción de flexión se puede controlar con precisión ajustando el tamaño del dibujo, logrando la precisión y el tamaño requerido por el diseño.
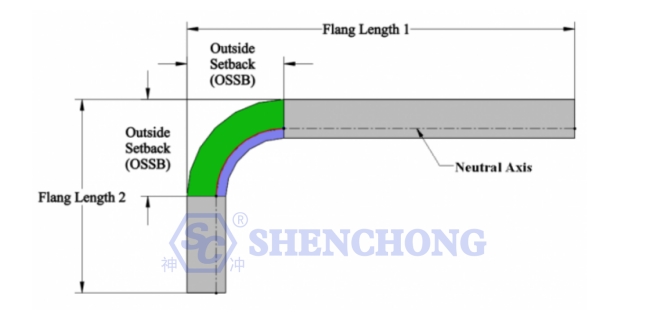
Según la figura anterior, la deducción por curvatura es la diferencia entre el margen de curvatura y el doble del retroceso exterior.
Fórmula de cálculo de deducción de curvatura
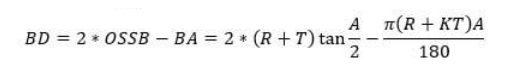
Dónde:
OSSB: el retroceso exterior (la longitud de la pieza que se extiende más allá del ángulo de plegado).
R – Radio de curvatura
K – Factor K (determinado por las propiedades y el espesor del material)
T – Espesor del material
A – Ángulo de curvatura deseado en grados
Supongamos que queremos doblar una lámina de acero inoxidable de 2 mm de espesor en un ángulo de 90° con un radio de curvatura interior de 3 mm. Se sabe que el factor K para este material es 0,44. Calculemos la Deducción por Doblez paso a paso:
- Calcule el margen de curvatura (BA):
BA = π * (R + K * T) * (A/180)
Donde R es el radio de curvatura interior, K es el factor K, T es el espesor de la lámina y A es el ángulo de curvatura.
Introduciendo los valores:
BA = π * (3 + 0,44 * 2) * (90/180) = 4,39 mm
- Calcule el retroceso exterior (OSSB):
OSSB = R + T = 3 + 2 = 5mm
- Calcule la deducción por curvatura (BD):
BD = 2 * OSSB – BA
Introduciendo los valores:
BD = 2 * 5 – 4,39 = 5,61 mm
Por lo tanto, para lograr una curvatura de 90° con un radio de curvatura interior de 3 mm en esta lámina de acero inoxidable de 2 mm de espesor, debemos establecer la Deducción de curvatura en 5,61 mm durante el proceso de curvatura.
Esto significa que debemos doblar la hoja en exceso 5,61 mm para compensar el retorno elástico después de doblarla y, en última instancia, lograr el ángulo de curvatura deseado de 90°.
El cálculo de la deducción por curvatura puede ayudar a determinar las dimensiones de la pieza antes de doblarla, lo que permite una mejor planificación de la producción y una reducción del desperdicio de material.
Funciones principales de la deducción por flexión
- Garantizar la precisión de flexión. La deducción de flexión puede controlar la longitud y el ángulo de la chapa doblada, garantizando así que las piezas de chapa producidas cumplan con los requisitos de tamaño y precisión del diseño.
- Mejorar la eficiencia del procesamiento. El diseño de deducción por flexión no solo reduce el tamaño de la producción, sino que también evita experimentos y ajustes repetidos, mejorando así la eficiencia de la fabricación de piezas de chapa metálica.
- Reducir el desperdicio de materiales. Al utilizar la deducción por flexión para controlar las dimensiones, se puede evitar el procesamiento excesivo o el desperdicio de material, reduciendo así los costos y mejorando la eficiencia de la producción.
En resumen, la deducción por flexión es un eslabón muy importante en el proceso de procesamiento de chapa y también es la clave para garantizar la calidad y precisión del producto terminado. En el procesamiento real, el valor de deducción de flexión debe ajustarse razonablemente según la situación específica para lograr el mejor efecto de procesamiento.
Materiales con diferente margen de curvatura
¿Qué metal se puede doblar bien?
Todos los metales tienen un cierto grado de elasticidad. Algunos metales son más elásticos que otros y pueden alcanzar mayores tolerancias a la flexión en comparación con otros materiales. Los metales se clasifican según su módulo de elasticidad, que es la relación entre la tensión y la deformación en la deformación del metal. El módulo de elasticidad también es un medio para medir la rigidez del material o la resistencia elástica. Otros materiales como el caucho y el vidrio también se pueden calcular del mismo modo.
Sorprendentemente, uno de los metales más elásticos es el níquel titanio, también conocido como níquel titanio, con una presión de 28 GPa. Se puede apretar muchas veces en gran medida sin que se considere deformado. Entre los tipos de metales comunes, los segundos metales elásticos más grandes incluyen 45 GPa de estaño, magnesio, cadmio y 69 GPa de aluminio. Por supuesto, el aluminio es conocido por su peso ligero y su capacidad de flexión, pero en términos de metales puros, incluidas las aleaciones, hay algunos metales que pueden superarlo en este sentido.
¿Qué metales no se pueden doblar bien o se fracturarán si se doblan demasiado?
Como es bien sabido, la mayoría de los metales son muy duros, y si el material no se dobla, definitivamente se fracturará al doblarse. Entre todas las aleaciones, el tungsteno es el metal más duro, alcanzando hasta 411 GPa. Incluso en su forma más delgada, el tungsteno es difícil de doblar, por lo que es probable que se rompa como el vidrio. El segundo metal más duro es el cobre-berilio de 304GPa. El cromo es un material que se encuentra en los diamantes y otras piedras preciosas y ocupa el tercer lugar con 279 GPa. Tanto el hierro forjado como el cobalto tienen 211 GPa. A 210 GPa, existen muchas más láminas de metal comunes, como acero, acero inoxidable, cobalto y níquel. Como sabes, la mayoría de los metales se consideran muy duros, pero como se mencionó anteriormente, algunos metales no son tan duros como otros.
Conclusión
El factor K, también conocido como factor de radio de curvatura, representa la tendencia del material a estirarse en la superficie exterior y comprimirse en la superficie interior durante la flexión.
El cálculo adecuado del factor K es importante para determinar la posición del eje neutro y minimizar posibles defectos como grietas o arrugas.
El margen de curvatura se refiere al material adicional necesario para adaptarse al radio de curvatura, evitando un estiramiento o compresión excesivos del material.
El cálculo preciso del margen de curvatura es vital para garantizar que las dimensiones finales de la pieza se alineen con las especificaciones de diseño.
La deducción de flexión, por otro lado, compensa el efecto elástico del material, donde la parte doblada tiende a enderezarse parcialmente después de que se elimina la fuerza de flexión.
Tener en cuenta la deducción de curvatura es esencial para lograr el ángulo de curvatura deseado y mantener la precisión dimensional.
Al comprender y aplicar adecuadamente estos factores esenciales, puede optimizar sus procesos de plegado, minimizar el desperdicio de material y producir constantemente componentes doblados de alta calidad que cumplan con los requisitos más estrictos.





