الأخبار و الأحداث

ما هو العامل K وبدل الانحناء وخصم الانحناء؟

مقدمة

يعد حساب عامل K الصحيح وبدل الانحناء وخصم الانحناء أمرًا بالغ الأهمية للحصول على جزء نهائي عالي الجودة من منزلك هيدروليكي اضغط على الفرامل. تعتبر المعرفة والتقنية الخاصة بمكابس الضغط من أساسياتها، والتي تعتبر ذات أهمية قصوى لمساعدتك في استخدامها في التصنيع.

إن حساب طول النموذج المسطح من الجزء ثلاثي الأبعاد ليس بالأمر الصعب حقًا. على الرغم من أنك قد تجد العديد من الصيغ المختلفة التي تدعي حساب بدل الانحناء، إلا أنها عادةً ما تكون نفس الصيغة، ويتم تبسيطها فقط عن طريق ملء الزاوية أو العامل K. ستوضح لك هذه المقالة هذه المعلومات، بما في ذلك العامل K وبدل الانحناء وخصم الانحناء.

ما هو بدل الانحناء؟

يمكن بالفعل ثني المعادن. عند تصنيع الصفائح المعدنية، يجب ثني المعدن، ليس فقط لتشكيل شكل معين، ولكن أيضًا للامتثال لأنظمة السلامة عندما يتعرض المعدن للصدمات، مما يجعله ينحني بدلاً من أن ينكسر. بغض النظر عن نوع المعدن، وكذلك شكل المعدن وسمكه، فإن كل قطعة معدنية لديها درجة معينة من بدل الانحناء.

تعريف بدل الانحناء

بدل الانحناء (BA) هو طول قوس الانحناء المقاس على طول المحور المحايد للوحة المعدنية حيث أن طول المحور المحايد لا يتغير بعد الانحناء.

بمجرد حساب بدل الانحناء، يجب إضافته إلى الطول المسطح لتحديد طول الصفائح المعدنية المطلوبة لتشكيل قطعة العمل المطلوبة.

كيفية حساب بدل الانحناء

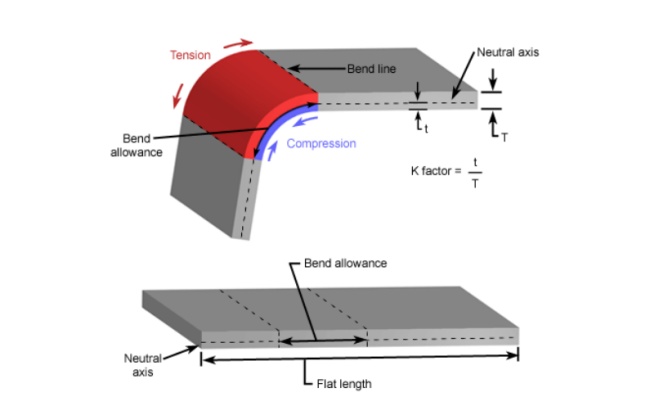
كما هو مبين في الشكل أدناه:

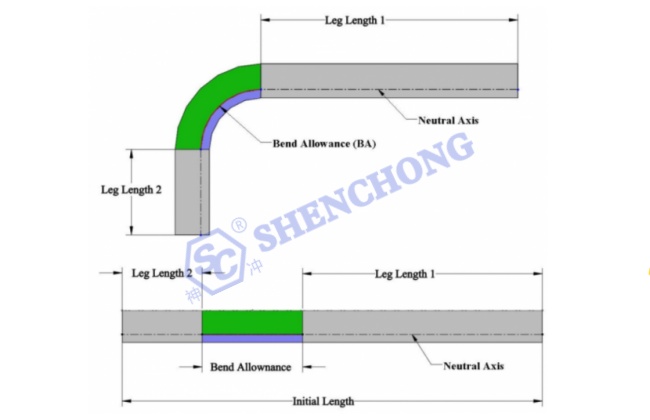
يتم استخدام الصيغة التالية لحساب الطول المسطح:

طول الصفائح المعدنية المسطحة = طول الساق 1 + BA + طول الساق 2

صيغة حساب بدل الانحناء

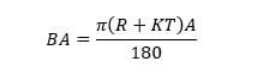
أ – زاوية الانحناء

R - نصف القطر الداخلي

عامل ك – ك

T – سمك المادة

لنبدأ بقوس L بسيط. توضح الصورة أن أرجل الدعامة يبلغ حجمها 2 بوصة و3 بوصة. سمك المادة 0.125"، نصف القطر الداخلي 0.250"، وزاوية الانحناء 90 درجة. الطول المسطح هو إجمالي الجزء المسطح من كلا الحافتين بالإضافة إلى الطول عبر قوس منطقة الانحناء. لكن، هل تحسب ذلك داخل المادة أم خارجها؟ لا! هذا هو المكان الذي يلعب فيه العامل K. العامل K هو النسبة المئوية لسمك المادة حيث لا يوجد تمدد أو ضغط للمادة، على سبيل المثال، المحور المحايد. بالنسبة إلى شريحة L البسيطة هذه، سأستخدم عامل K بقيمة 0.42.

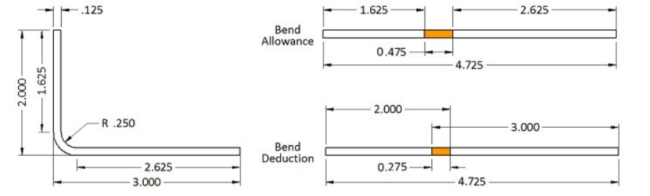
باستخدام الصيغة أعلاه، لدينا: بدل الانحناء = 90 * (π / 180) * (0.250 + 0.42 * 0.125) = 0.475″.

وبالتالي فإن طول النمط المسطح هو 1.625 بوصة + 2.625 بوصة + 0.475 بوصة وهو ما يساوي 4.725 بوصة. لذا، إذا قمت بإضافة الطول المسطح لجميع الحواف وأضفت بدل انحناء واحد لكل منطقة انحناء، فستحصل على الطول المسطح الصحيح للجزء.

لكن انظر إلى الرسم. ليست هذه هي الطريقة التي نقوم بها عادة بقياس جزء من الصفائح المعدنية. تكون الأبعاد عادةً عند تقاطع الفلنجات أو خط القالب. هذا يعني أنه يتعين علينا طرح ضعف سمك المادة بالإضافة إلى نصف قطر الانحناء (المعروف أيضًا باسم النكسة) لكل منطقة انحناء. بالنسبة لهذه المجموعة من الأبعاد، سيكون من الأسهل حساب قيمة تعويض الانحناء. تتيح لك قيمة تعويض الانحناء إضافة طول كل شفة باستخدام أبعاد خط القالب ثم إضافة تعويض انحناء واحد لكل منطقة انحناء إلى الإجمالي. إنه -0.275، وهو رقم سالب، مما يعني أنك ستطرح هذا المبلغ من إجمالي أطوال الفلنجة، 5 بوصات، لتحصل على 4.725 بوصة.

ما هو العامل K؟

العامل k هو النسبة المئوية لسمك المادة حيث لا يوجد تمدد أو ضغط للمادة في منطقة الانحناء.

كلما كانت المادة أكثر صلابة، قل الضغط الموجود داخل الانحناء. ولذلك، فإن المزيد من التمدد من الخارج ويتحرك المحور المحايد نحو داخل الانحناء. تسمح المواد الأكثر ليونة بمزيد من الضغط من الداخل ويظل المحور المحايد أقرب إلى مركز سمك المادة.

نصف قطر الانحناء له تأثير مماثل. كلما كان نصف قطر الانحناء أصغر، زادت الحاجة إلى الضغط ويتحرك المحور المحايد نحو داخل الانحناء. على دائرة نصف قطرها أكبر. يبقى المحور المحايد بالقرب من مركز سمك المادة.

لفهم العامل K، علينا أولاً أن نفهم المحور المحايد.

عندما يتم ثني الصفائح المعدنية، يتم ضغط السطح السفلي، ويتم تمديد السطح العلوي. يقع المحور المحايد داخل المعدن حيث لن يتم ضغطه أو توسيعه، مما يسمح له بالحفاظ على طول ثابت.

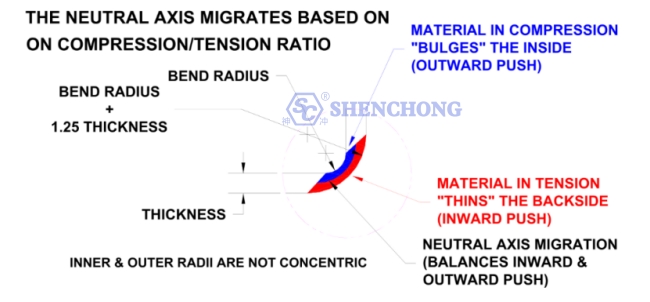
المحور المحايد

المحور المحايد لا يتغير. عند تطوير طول فارغ مسطح، هناك طول للجزء لا يتغير، ويسمى هذا الطول بالمحور المحايد. سوف تنضغط المادة الموجودة داخل المحور المحايد، بينما ستتمدد المادة الموجودة بالخارج. بناءً على نصف قطر شكل سمك المادة وطرق التشكيل، تتغير نسبة الضغط إلى الشد في الجزء.

الجزء الذي يتم ثنيه على نصف قطر حاد جدًا، عند مقارنته بالسمك، سوف يتمدد أكثر من الخارج، مما يعني أن المحور المحايد سيكون أقرب إلى داخل الانحناء. الجزء الذي يتم ثنيه تدريجيًا سيكون له امتداد خارجي أقل، مما يعني أن المحور المحايد سيكون أقرب إلى مركز الجزء.

في الصفائح المعدنية المسطحة، يقع المحور المحايد بالتساوي عند نصف سمك الصفائح المعدنية، لكنه سيتحرك أثناء الثني.

يتم تحديد تغيير موضع المحور المحايد من خلال عوامل مختلفة مثل خصائص المادة والسمك وزاوية الانحناء ونصف القطر الداخلي وطريقة ثني اللوحة.

كيفية حساب العوامل K

رياضياً، يمثل العامل K النسبة بين موضع المحور المحايد (t) وسمك اللوحة (T).

صيغة العوامل K

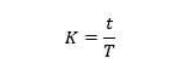
حيث t هي المسافة من السطح الداخلي إلى المحور المحايد و T هو سمك المعدن.

يتم تحديد العامل K من خلال الخصائص الفيزيائية للمادة وطريقة الانحناء وزاوية الانحناء وعوامل أخرى.

ستكون قيمة عوامل K دائمًا بين 0 و1. إذا كان عامل ak هو 0.25، فهذا يعني أن المحور المحايد يقع عند 25% من سمك مادة الصفائح المعدنية للجزء. وبالمثل، إذا كانت 0.5، فهذا يعني أن المحور المحايد يقع عند 50% من السماكة بأكملها.

خصائص المواد: يتراوح عادة بين 0.30 و 0.50. بشكل عام، العامل K للنحاس الناعم أو المواد النحاسية الناعمة هو 0.35، والعامل K للمواد مثل النحاس شبه الصلب أو النحاس الأصفر والفولاذ الطري والألومنيوم هو 0.41، والعامل K للمواد مثل البرونز، النحاس الصلب والفولاذ المدلفن على البارد والفولاذ الزنبركي 0.45.

نصف قطر الانحناء: كلما كان نصف قطر الانحناء أصغر، كلما زاد العامل K.

سمك المادة: كلما زاد سمك المادة، كلما زاد العامل K.

قوة الخضوع للمواد: كلما زادت قوة الخضوع، كلما كان العامل K أصغر.

معامل المرونة (المعروف أيضًا باسم معامل يونج): كلما زاد سمك المادة، كلما زاد العامل K.

في تصنيع الصفائح المعدنية الدقيقة باستخدام الفرامل الصحافة باستخدام الحاسب الآلي، العامل K هو عامل حاسم. يتم استخدام العامل K لحساب نمط الانحناء المسطح، والذي يرتبط بشكل مباشر بطول الصفائح المعدنية التي تم تمديدها أثناء الثني.

إنها القيمة الأساسية لتحديد بدل الانحناء وخصم الانحناء.

نظرًا لأن نسبة المسافة إلى المحور المحايد إلى سمك اللوحة تحدد موضع المحور المحايد في اللوحة المعدنية، فإن معرفة العامل K يساعد في تحديد موضع المحور المحايد بعد الثني.

عوامل K للألمنيوم والصلب

يمكنك أيضًا تحديد العامل K باستخدام الجدول أدناه:

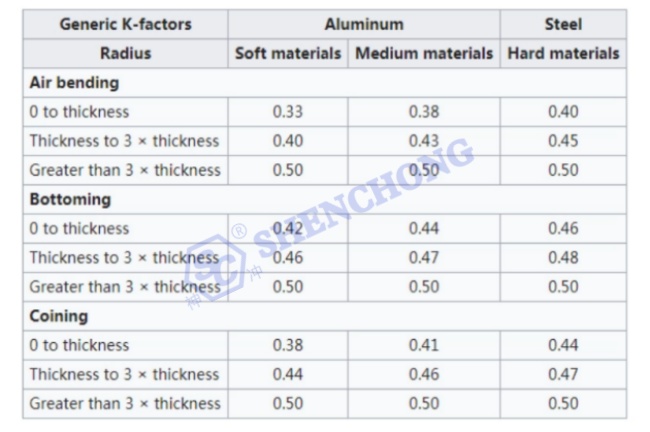
عوامل K للنحاس والنحاس والبرونز

وبعد دراسة متأنية، وجد أن نظام SolidWorks يوفر أيضًا خوارزميات تعويض الانحناء للمواد المحددة التالية بزاوية انحناء قدرها 90 درجة. صيغة الحساب المحددة هي كما يلي:

النحاس الناعم أو مادة النحاس الناعمة: BA=(0.55 * T)+(1.57 * R)

مواد مثل النحاس أو النحاس شبه الصلب والفولاذ الناعم والألمنيوم: BA=(0.64 * T)+(1.57 * R) مواد مثل البرونز والنحاس الصلب والفولاذ المدلفن على البارد والفولاذ الزنبركي: BA=(0.71 * T)+(1.57 * R) في الواقع، إذا قمنا بتبسيط المعادلة (7) وجعلنا زاوية الانحناء 90 درجة وحساب الثابت، فيمكن تحويل المعادلة إلى:

با=(1.57 * ك * تي)+(1.57 * ر)

لذلك، بالنسبة للنحاس الناعم أو المواد النحاسية الناعمة، من خلال مقارنة صيغة الحساب المذكورة أعلاه، يمكننا الحصول على 1.57xK=0.55K=0.55/1.57=0.35. من السهل حساب قيم العامل k لعدة أنواع من المواد المدرجة في الكتاب باستخدام نفس الطريقة.

النحاس الناعم أو مادة النحاس الناعمة: K=0.35.

مواد مثل النحاس أو النحاس شبه الصلب والفولاذ الناعم والألومنيوم: K = 0.41.

مواد مثل البرونز والنحاس الصلب والفولاذ المدرفل على البارد والفولاذ الزنبركي: K=0.45.

ما هو خصم الانحناء؟

عند ثني الصفائح المعدنية، بسبب التشوه البلاستيكي غير الكامل للمادة والقيود الهيكلية لأداة الآلة نفسها، قد تنحرف زاوية وطول قطعة العمل المنحنية عن الأبعاد المصممة. من أجل ضمان دقة الانحناء وحجم قطعة العمل التي تلبي المتطلبات، من الضروري مراعاة خصم الانحناء أثناء إنتاج الرسم، أي تقليل حجم الانحناء الذي يجب القيام به.

تعريف خصم الانحناء

خصم الانحناء هو طول المادة التي نحتاج إلى إزالتها من الطول الإجمالي للوحة للحصول على النمط المسطح الصحيح.

مبدأ خصم الانحناء

مبدأ خصم الانحناء هو استخدام التشوه المرن للمادة، بحيث يمكن للطول والزاوية بعد الانحناء تلبية متطلبات التصميم. عند الثني، يتم وضع الصفائح المعدنية على آلة الثني، والتي تطبق قوة الثني لتسبب تشوهًا مرنًا للصفائح المعدنية، مما يؤدي إلى تغيرات في الشكل والزاوية، وفي النهاية تصبح الشكل المطلوب. في هذه العملية، يمكن التحكم بدقة في خصم الانحناء عن طريق ضبط حجم الرسم، وتحقيق الدقة والحجم الذي يتطلبه التصميم.

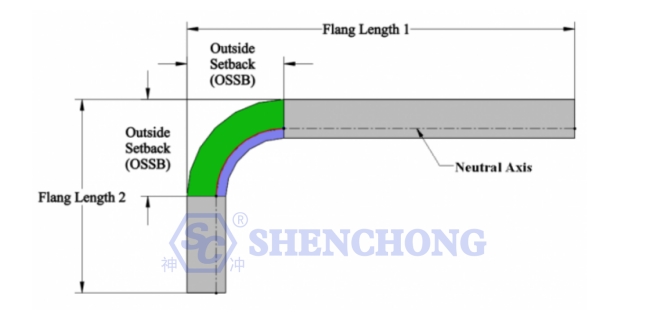
وفقا للشكل أعلاه، فإن خصم الانحناء هو الفرق بين بدل الانحناء وضعف النكسة الخارجية.

صيغة حساب خصم الانحناء

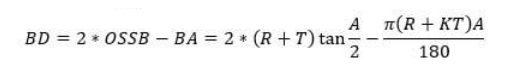
أين:

OSSB – النكسة الخارجية (طول الجزء الذي يمتد إلى ما بعد زاوية الانحناء).

R - نصف قطر الانحناء

K - عامل K (يتم تحديده حسب خصائص المادة وسمكها)

T – سمك المادة

أ - زاوية الانحناء المطلوبة بالدرجات

لنفترض أننا نريد ثني لوح من الفولاذ المقاوم للصدأ بسمك 2 مم بزاوية 90 درجة مع نصف قطر انحناء داخلي يبلغ 3 مم. من المعروف أن العامل K لهذه المادة هو 0.44. دعونا نحسب خصم الانحناء خطوة بخطوة:

حساب بدل الانحناء (BA):

با = π * (R + K * T) * (أ / 180)

حيث R هو نصف قطر الانحناء الداخلي، وK هو العامل K، وT هو سمك الورقة، وA هي زاوية الانحناء.

توصيل القيم:

BA = π * (3 + 0.44 * 2) * (90 / 180) = 4.39 ملم

حساب النكسة الخارجية (OSSB):

OSSB = R + T = 3 + 2 = 5 مم

حساب خصم الانحناء (BD):

دينار بحريني = 2 * OSSB – BA

توصيل القيم:

دينار بحريني = 2*5 – 4.39 = 5.61 ملم

لذلك، لتحقيق انحناء بمقدار 90 درجة مع نصف قطر انحناء داخلي 3 مم على لوح الفولاذ المقاوم للصدأ بسمك 2 مم، نحتاج إلى ضبط خصم الانحناء على 5.61 مم أثناء عملية الثني.

هذا يعني أننا بحاجة إلى ثني الصفيحة بشكل زائد بمقدار 5.61 مم للتعويض عن الزنبرك الخلفي بعد الثني، وبالتالي تحقيق زاوية الانحناء المطلوبة البالغة 90 درجة.

يمكن أن يساعد حساب خصم الانحناء في تحديد أبعاد الأجزاء قبل الثني، مما يسمح بتخطيط إنتاج أفضل وتقليل هدر المواد.

الوظائف الرئيسية لخصم الانحناء

التأكد من دقة الانحناء. يمكن لخصم الانحناء التحكم في طول وزاوية الصفائح المعدنية المنحنية، وبالتالي ضمان أن أجزاء الصفائح المعدنية المنتجة تلبي متطلبات الحجم والدقة للتصميم.
تحسين كفاءة المعالجة. لا يؤدي تصميم خصم الانحناء إلى تقليل حجم الإنتاج فحسب، بل يتجنب أيضًا التجارب والتعديلات المتكررة، وبالتالي تحسين كفاءة تصنيع أجزاء الصفائح المعدنية.
تقليل النفايات المادية. باستخدام خصم الانحناء للتحكم في الأبعاد، يمكن تجنب المعالجة المفرطة أو هدر المواد، وبالتالي تقليل التكاليف وتحسين كفاءة الإنتاج.

باختصار، يعد خصم الانحناء رابطًا مهمًا جدًا في عملية معالجة الصفائح المعدنية، وهو أيضًا المفتاح لضمان جودة ودقة المنتج النهائي. في المعالجة الفعلية، يجب تعديل قيمة خصم الانحناء بشكل معقول وفقًا للحالة المحددة لتحقيق أفضل تأثير للمعالجة.

المواد ذات بدل الانحناء المختلفة

ما هو المعدن الذي يمكن أن ينحني جيدًا؟

جميع المعادن لديها درجة معينة من المرونة. بعض المعادن أكثر مرونة من غيرها وقد تحقق بدلات انحناء أكبر مقارنة بالمواد الأخرى. يتم تصنيف المعادن وفقًا لمعامل المرونة الخاص بها، وهو النسبة بين الإجهاد والانفعال في تشوه المعدن. المعامل المرن هو أيضًا وسيلة لقياس صلابة المادة أو المقاومة المرنة. ويمكن أيضًا حساب المواد الأخرى مثل المطاط والزجاج بنفس الطريقة.

من المثير للدهشة أن أحد أكثر المعادن مرونة هو النيكل والتيتانيوم، المعروف أيضًا باسم النيكل والتيتانيوم، حيث يبلغ ضغطه 28 جيجا باسكال. ويمكن شدها عدة مرات إلى حد كبير دون أن تعتبر مشوهة. من بين أنواع المعادن الشائعة، ثاني أكبر المعادن المرنة تشمل 45 جيجا باسكال من القصدير والمغنيسيوم والكادميوم و69 جيجا باسكال من الألومنيوم. بالطبع، الألمنيوم معروف بخفة وزنه وقدرته على الانحناء، لكن فيما يتعلق بالمعادن النقية، بما في ذلك السبائك، هناك بعض المعادن التي يمكن أن تتفوق عليه في هذا الصدد.

ما هي المعادن التي لا يمكن أن تنحني جيدًا، أو أنها تنكسر عندما تنحني كثيرًا؟

وكما هو معروف، فإن معظم المعادن شديدة الصلابة، وإذا لم يتم ثني المادة، فإنها بالتأكيد سوف تنكسر عند الثني. من بين جميع السبائك، يعتبر التنغستن هو المعدن الأكثر صلابة، حيث يصل إلى 411 جيجا باسكال. حتى في أنحف أشكاله، يصعب ثني التنغستن، لذلك من المحتمل أن ينكسر مثل الزجاج. ثاني أصلب معدن هو 304GPa نحاس البريليوم. الكروم هو مادة موجودة في الألماس والأحجار الكريمة الأخرى، وتحتل المرتبة الثالثة بـ 279 جيجا باسكال. يحتوي كل من الحديد المطاوع والكوبالت على 211 جيجا باسكال. في 210 جيجا باسكال، لديك العديد من الصفائح المعدنية الشائعة، مثل الفولاذ والفولاذ المقاوم للصدأ والكوبالت والنيكل. كما تعلم، تعتبر معظم المعادن شديدة الصلابة، ولكن كما ذكرنا سابقًا، فإن بعض المعادن ليست بنفس صلابة غيرها.

خاتمة

العامل K، المعروف أيضًا باسم عامل نصف قطر الانحناء، يفسر ميل المادة إلى التمدد على السطح الخارجي والضغط على السطح الداخلي أثناء الانحناء.

يعد الحساب الصحيح للعامل K مهمًا لتحديد موضع المحور المحايد وتقليل العيوب المحتملة مثل التشقق أو التجاعيد.

يشير بدل الانحناء إلى المادة الإضافية المطلوبة لاستيعاب نصف قطر الانحناء، مما يمنع التمدد المفرط أو ضغط المادة.

يعد الحساب الدقيق لبدل الانحناء أمرًا حيويًا لضمان توافق أبعاد الجزء النهائي مع مواصفات التصميم.

من ناحية أخرى، يعوض خصم الانحناء تأثير الزنبرك الخلفي للمادة، حيث يميل الجزء المنحني إلى عدم الانحناء جزئيًا بعد إزالة قوة الانحناء.

يعد حساب خصم الانحناء أمرًا ضروريًا لتحقيق زاوية الانحناء المطلوبة والحفاظ على دقة الأبعاد.

من خلال فهم هذه العوامل الأساسية وتطبيقها بشكل صحيح، يمكنك تحسين عمليات الثني الخاصة بها، وتقليل هدر المواد، وإنتاج مكونات منحنية عالية الجودة بشكل متسق تلبي المتطلبات الأكثر صرامة.

مقالات ذات صلة:

حساب حمولة الفرامل

أفضل 8 مصنعين لآلات القطع بالليزر

أفضل 12 مصنعًا لآلات CNC

تصنيف أفضل العلامات التجارية لآلات ضغط الفرامل في الصين

كل ما تحتاج لمعرفته حول مقياس الصفائح المعدنية